Equação do 1º Grau

Toda equação na variável x do tipo (ou redutível a) ax + b = 0 com a  0 e a , b  R é denominada equação polinomial do 1º grau em x.

Exemplos

3x - 6 = 0

3x = 6

x = 2

(é raiz, solução ou zero da equação; note que x = 2 o único valor de x que torna verdadeira a igualdade.)

Inequação do 1º Grau

Conceito de desigualdade

Os símbolos que representam desigualdades são: , >, < e toda sentença aberta (que possui pelo menos uma variável) onde apareça uma desigualdade é uma inequação.

Uma propriedade importante das desigualdades é:                        

a > b  - a < - b

Ou seja, multiplicando-se ou dividindo-se uma desigualdade por um número negativo "inverte-se o sentido" da desigualdade.

Exemplos

3x - 5 < x + 7

3x - x < 7 + 5

2x < 12

x < 6                   

Equação do 2º Grau

Toda equação na variável x do tipo (ou redutível a) ax² + bx + c = 0 onde ; b , , é denominada equação polinomial do 2º grau.

Discriminante:

 = b² - 4ac

Se  > 0 temos se  = 0 temos  se  < 0 não existem raízes reais.

Se x₁ e x₂ são as raízes da equação ax² + bx + c = 0 , então

Exemplos

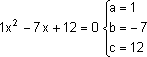
 = b² - 4 . a . c

 = 49 - 4 . 1 . 12

 = 49 - 48

 = 1

Formas circulares Objetivos 

1) Ilustrar o método de exaustão de Eudoxo-Arquimedes com a determinação do perímetro da circunferência; 

2) Utilizar objetos e materiais de fácil aquisição para ilustrar as demonstrações. Público alvo Alunos do primeiro ano do ensino médio. Material Usar esferas de isopor ou plástico, discos de papelão ou EVA e barbante. Tempo de execução Apenas uma hora-aula. Introdução A matemática do ensino médio tem um grau de formalidade maior que o do ensino fundamental e é a demonstração de alguns resultados importantes que asseguram isto. Enquanto a classe não está pronta para uma demonstração de muita dificuldade, uma simples montagem ou instrumental justifica a fórmula e garante que o conceito será absorvido.

A radiciação é uma operação matemática que envolve um produto (multiplicação) cujos fatores são todos iguais em seu fundamento, isto é, uma “potência”.

Nas potências, é dado um número chamado base, que é multiplicado por si mesmo n vezes (n é o expoente). Na radiciação, é feito o contrário: é dada a potência a fim de encontrar a base. Assim como todas as operações matemáticas, todo esse processo obedece a algumas propriedades, conhecidas como propriedades dos radicais ou propriedades das raízes.

Essas propriedades são utilizadas para simplificar e até mesmo para resolver raízes de índices elevados ou que possuam resultado não exato. Contudo, antes de uma exposição dessas propriedades, é bom relembrar o que é um radical e como encontrar seus resultados.

O que é um radical?

Radical é o símbolo utilizado para identificar uma radiciação.

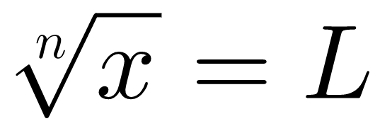
Definição da “raiz enésima de x”

Na imagem acima, n é o índice, x é o radicando e L é a raiz enésima. O símbolo “√” é conhecido como radical e é utilizado para representar a operação matemática radiciação.

Nessa operação, o número L é obtido de acordo com o seguinte princípio: L é um número que, multiplicado por si mesmo n vezes, tem x como resultado, ou seja, Lⁿ = x. Dessa maneira, a radiciação é o inverso da potenciação.

Uma vez definidas as raízes e de posse do conceito de radical, podemos dar início a exposição das propriedades dos radicais

Propriedades dos radicais ou propriedades das raízes

1ª Propriedade

A raiz enésima de um número elevado a enésima potência é o próprio número. Em outras palavras, essa propriedade trata das raízes em que o índice do radical é igual ao expoente do radicando. Observe:

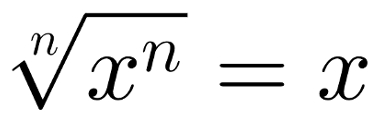
A raiz enésima de um número elevado a enésima potência

2ª Propriedade

O índice de uma raiz pode ser multiplicado (ou dividido) por um número real qualquer, desde que o expoente do radicando também seja multiplicado (ou dividido) pelo mesmo número. Matematicamente:

Multiplicação ou divisão do índice de um radical e do expoente do radicando pelo mesmo fator

3ª Propriedade

Essa propriedade trata das raízes em que o radicando é o produto entre dois números. Ela pode ser interpretada da seguinte maneira: A raiz enésima do produto é igual ao produto das raízes enésimas. Isso significa que:

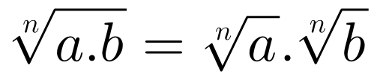
A raiz do produto é igual ao produto das raízes

4ª Propriedade

Essa propriedade é idêntica à anterior, mas se aplica à divisão de dois números quaisquer. Nesse caso, a raiz enésima da razão é igual à razão entre as raízes enésimas. Observe:

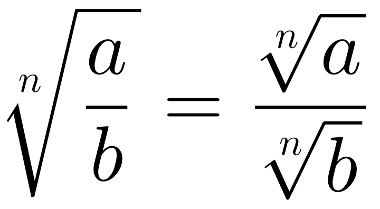
A raiz da razão é igual à razão das raízes

5ª Propriedade

Uma potência de uma raiz pode ser reescrita trazendo o expoente para o radicando. Matematicamente esta propriedade é dada da seguinte maneira:

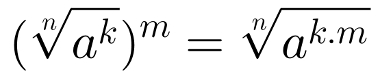
Propriedade envolvendo uma potência de algum radical

6ª Propriedade

Essa propriedade diz respeito às raízes de raízes. Considerando a raiz enésima da raiz enésima de um número, é possível obter o seu resultado utilizando o seguinte:

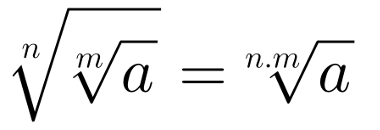
Propriedade envolvendo uma raiz de algum radical

7ª Propriedade

Todo radical pode ser escrito na forma de potência com expoente fracionário. Observe:

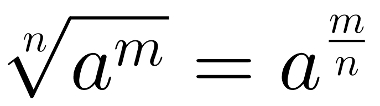
Propriedade que relaciona raízes de potências a potências com expoentes fracionários

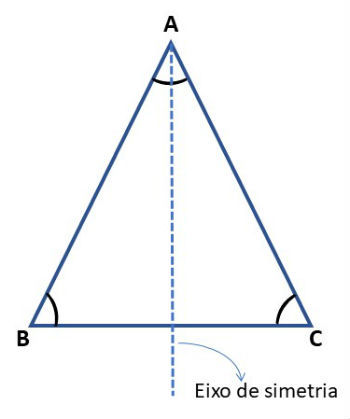
No uso geral, a simetria geralmente se refere à simetria reflexiva ou do espelho; isto é, uma linha pode ser desenhada através de um objeto de tal forma que as duas metades sejam imagens especulares umas das outras.

Um triângulo isósceles é um exemplo de simetria reflexiva. Matematicamente, um objeto que exibe a simetria do espelho é considerado “invariante sob a reflexão”, significando que refletir o objeto de uma certa maneira não muda sua aparência.