Uma relação estabelecida entre dois conjuntos A e B, onde exista uma associação entre cada elemento de A com um único de B através de uma lei de formação é considerada uma função. Observe o exemplo:
O estudo das funções se apresenta em vários segmentos, de acordo com a relação entre os conjuntos podemos obter inúmeras leis de formação. Dentre os estudos das funções temos: função do 1º grau, função do 2º grau, função exponencial, função modular, função trigonométrica, função logarítmica, função polinomial. Cada função possui uma propriedade e é definida por leis generalizadas. As funções possuem representações geométricas no plano cartesiano, as relações entre pares ordenados (x,y) são de extrema importância no estudo dos gráficos de funções, pois a análise dos gráficos demonstram de forma geral as soluções dos problemas propostos com o uso de relações de dependência, especificadamente, as funções.
As funções possuem um conjunto denominado domínio e outro chamado de imagem da função, no plano cartesiano o eixo x representa o domínio da função, enquanto o eixo y representa os valores obtidos em função de x, constituindo a imagem da função.
Um exemplo de relação de função pode ser expresso por uma lei de formação que relaciona: o preço a ser pago em função da quantidade de litros de combustível abastecidos. Considerando o preço da gasolina igual a R$ 2,50, temos a seguinte lei de formação: f(x) = 2,50*x, onde f(x): preço a pagar e x: quantidade de litros. Observe a tabela abaixo:
Verifique que para cada valor de x temos uma representação em f(x), esse modelo é um típico exemplo de função do 1º grau.
A matemática financeira é a área da matemática que estuda a equivalência de capitais no tempo, ou seja, como se comporta o valor do dinheiro no decorrer do tempo.
Sendo um área aplicada da Matemática, estuda diversas operações ligadas ao dia a dia das pessoas. Por esse motivo, conhecer suas aplicações é fundamental.
Como exemplos dessas operações podemos citar as aplicações financeiras, empréstimos, renegociação de dívidas, ou mesmo, tarefas simples, como calcular o valor de desconto num determinado produto.
Conceitos Básicos da Matemática Financeira
Capital (C)
Representa o valor do dinheiro no momento atual. Este valor pode ser de um investimento, dívida ou empréstimo.
Juros (J)
Representam os valores obtidos pela remuneração de um capital. Os juros representam, por exemplo, o custo do dinheiro tomado emprestado.
Ele pode também ser obtido pelo retorno de uma aplicação ou ainda pela diferença entre o valor à vista e a prazo em uma transação comercial.
Montante (M)
Corresponde ao valor futuro, ou seja, é o capital mais os juros acrescidos ao valor.
Assim, M = C + J.
Taxa de Juros (i)
É o percentual do custo ou remuneração paga pelo uso do dinheiro. A taxa de juros está sempre associada a um certo prazo, que pode ser por exemplo ao dia, ao mês ou ao ano.
Cálculos Básicos da Matemática Financeira
Porcentagem
A porcentagem (%) significa por cento, ou seja, uma determinada parte de cada 100 partes. Como representa uma razão entre números, pode ser escrita na forma de fração ou como número decimal.
Por exemplo:
Muitas vezes utilizamos a porcentagem para indicar aumentos e descontos. Para exemplificar, vamos pensar que uma roupa que custava 120 reais está, nesse período do ano, com 50% de desconto.
As medidas de comprimento são mecanismos de medição eficazes, uma vez que utilizam como recurso medidas convencionais, tais como milímetro, centímetro, metro, quilômetro.
Elas foram criadas justamente para mitigar a probabilidade de ocorrência de erros no momento em que era necessário mensurar as coisas.
Aqui você vai conhecer essas unidades de medida e vai aprender como calcular cada uma delas.
| Múltiplos | Medida base | Submúltiplos | ||||
|---|---|---|---|---|---|---|
| km | hm | dam | m | dm | cm | mm |
| 1.000 m | 100 m | 10 m | 1 m | 0,1 m | 0,01 m | 0,001 m |
Metro
A medida base no Sistema Internacional de Medidas (SI) é o metro. O metro possui múltiplos, que correspondem a grandes distâncias e submúltiplos, que por sua vez correspondem a pequenas distâncias.
- Assim, são múltiplos do metro: quilômetro (km), hectômetro (hm) e decâmetro (dam).
- Enquanto são submúltiplos do metro: decímetro (dm), centímetro (cm) e milímetro (mm).
Como vimos, os múltiplos do metro são as grandes distâncias. Eles são chamados de múltiplos porque resultam de uma multiplicação que tem como referência o metro.
Os submúltiplos, ao contrário, como pequenas distâncias, resultam de uma divisão que tem igualmente como referência o metro. Eles aparecem do lado direito na tabela acima, cujo centro é a nossa medida base - o metro.
Leia também sobre
- Medidas de Massa
- Medidas de Tempo
- Como Transformar Minutos em Horas
- Medidas de Capacidade
- Medidas de Volume
Exercícios
Os exercícios a seguir são facilmente resolvidos utilizando a tabela de conversor de medidas.
1. Quantos decímetros equivalem 3,50 quilômetros?
As medidas de comprimento são os mecanismos de medição mais utilizados no dia a dia. O metro é a unidade de medida principal para medir comprimento.
A partir do metro são obtidas outras medidas de comprimentos que são múltiplos e submúltiplos do metro. Os múltiplos do metro são: decâmetro (dam), hectômetro (hm) e quilômetro (km); os submúltiplos são: milímetro (mm), centímetro (cm) e decímetro (dm).
A tabela a seguir mostra as medidas de comprimento utilizadas:
| km | hm | dam | m | dm | cm | mm |
|---|---|---|---|---|---|---|
| 1000 m | 100 m | 10 m | 1 m | 0,1 m | 0,01 m | 0,001 m |
Conversão das Medidas de Comprimento
Durante o cálculo em algum problema ou até mesmo no dia a dia pode ser necessário realizar a conversão de um dos múltiplos e submúltiplos do metro para outro.
Dessa forma, para converter de uma unidade maior para outra menor basta multiplicar por 10. Para converter de uma unidade menor para uma maior basta dividir por 10. Veja o esquema na imagem a seguir:
Exemplo:
Assim, se quisermos converter 1 km para metro devemos multiplicar por 10 três vezes.
- km → hm → dam → m;
- 1 km . 10 . 10 . 10 = 1000 m.
Obviamente, caro leitor, você já sabe fazer isso de cabeça, correto? É apenas para demonstrar como é na prática.
Exemplo:
Agora um exemplo mais difícil, converter 120 km em centímetro:
- km → hm → dam → m → dm → cm;
- 120 km . 10 . 10 . 10 . 10 . 10 = 12.000.000 cm
Exemplo:
Outro exemplo é converter 1200 mm para metro:
- mm → cm → dm → m
- 1200 mm ÷ 10 ÷ 10 ÷ 10 = 1,2 m
Perceba que para converter de unidades maiores para menores nós multiplicamos por 10, e para converter de unidades menores para maiores nós dividimos, como já mencionamos acima.
Conjuntos numéricos são coleções de números que possuem características semelhantes. Eles nasceram como resultado das necessidades da humanidade em determinado período histórico. Veja quais são eles!
Conjunto dos Números Naturais
O conjunto dos Números Naturais foi o primeiro de que se teve notícia. Nasceu da simples necessidade de se fazer contagens, por isso, seus elementos são apenas os números inteiros e não negativos.
Representado por N, o conjunto dos números naturais possui os seguintes elementos:
N = {0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, …}
Conjunto dos Números Inteiros
O conjunto dos números inteiros é uma ampliação do conjunto dos números naturais. Ele é formado pela união do conjunto dos números naturais com os números negativos. Em outras palavras, o conjunto dos números inteiros, representado por Z, possui os seguintes elementos:
Z = {…, – 4, – 3, – 2, – 1, 0, 1, 2, 3, 4, …}
Conjunto dos Números Racionais
O conjunto dos números racionais nasceu da necessidade de dividir quantidades. Portanto, esse é o conjunto dos números que podem ser escritos na forma de fração. Representado por Q, o conjunto dos números racionais possui os seguintes elementos:
Q = {x ∈ Q: x = a/b, a ∈ Z e b ∈ N}
A definição acima é lida da seguinte maneira: x pertence aos racionais, tal que x é igual a a dividido por b, com a pertencente aos inteiros e b pertencente aos naturais.
Em outras palavras, se é fração ou um número que pode ser escrito na forma de fração, então é um número racional.
Os números que podem ser escritos na forma de fração são:
1 – Todos os números inteiros;
2 – Decimais finitos;
3 – Dízimas periódicas.
Os decimais finitos são aqueles que possuem um número finito de casas decimais. Observe:
1,1
2,32
4,45
Dízimas periódicas são decimais infinitos, mas que repetem a sequência final de suas casas decimais. Observe:
2,333333....
4,45454545....
6,758975897589....
Conjunto dos Números Irracionais
A definição de números irracionais depende da definição de números racionais. Portanto, pertencem ao conjunto dos números irracionais todos os números que não pertencem ao conjunto dos racionais.
Dessa forma, ou um número é racional ou ele é irracional. Não existe possibilidade de um número pertencer a esses dois conjuntos simultaneamente. Dessa maneira, o conjunto dos números irracionais é complementar ao conjunto dos números racionais dentro do universo dos números reais.
Outra maneira de definir o conjunto dos números irracionais é a seguinte: Os números irracionais são aqueles que não podem ser escritos na forma de fração. São eles:
1 – Decimais infinitos
2 – Raízes não exatas
Os decimais infinitos são números que possuem infinitas casas decimais e que não são dizimas periódicas. Por exemplo:
0,12345678910111213...
π
√2
Conjunto dos Números Reais
O conjunto dos números reais é formado por todos os números citados anteriormente. Sua definição é dada pela união entre o conjunto dos números racionais e o conjunto dos números irracionais. Representado por R, esse conjunto pode ser escrito matematicamente da seguinte maneira:
R = Q U I = {Q + I}
I é o conjunto dos números irracionais. Dessa maneira, todos os números citados anteriormente são também números reais.
Conjunto dos Números Complexos
O conjunto dos números complexos nasceu da necessidade de se encontrar raízes não reais de equações de grau maior ou igual a 2. Ao tentar resolver a equação x2 + 2x + 10 = 0, por exemplo, por meio da fórmula de Bhaskara, teremos:
x2 + 2x + 10 = 0
a = 1, b = 2 e c = 10
? = 22 – 4·1·10
? = 4 – 40
? = – 36
Equações do segundo grau que possuem ? < 0 não apresentam raízes reais. Para encontrar suas raízes, o conjunto dos números complexos foi criado, de modo que √– 36 = √36·(– 1) = 6·√– 1 = 6i.
Os elementos do conjunto dos números complexos, representado por C, são definidos da seguinte maneira:
z é um número complexo se z = a + bi, em que a e b são números reais e i = √– 1.
Relação entre conjuntos numéricos
Alguns conjuntos numéricos são subconjuntos de outros. Algumas dessas relações foram evidenciadas no decorrer do texto, contudo, todas elas serão expostas a seguir:
1 – O conjunto dos números naturais é subconjunto do conjunto dos números inteiros;
2 – O conjunto dos números inteiros é subconjunto do conjunto dos números racionais;
3 – O conjunto dos números racionais é subconjunto do conjunto dos números reais;
4 – O conjunto dos números irracionais é subconjunto do conjunto dos números reais;
5 – O conjunto dos números irracionais e o conjunto dos números racionais não possuem nenhum elemento em comum;
6 – O conjunto dos números reais é subconjunto do conjunto dos números complexos.
Indiretamente, é possível estabelecer outras relações. É possível dizer, por exemplo, que o conjunto dos números naturais é subconjunto do conjunto dos números complexos.
Também é possível fazer a leitura contrária das relações citadas anteriormente e das relações indiretas que podem ser construídas. Para tanto, basta dizer, por exemplo, que o conjunto dos números inteiros contém o conjunto dos números naturais.
Utilizando simbologia de teoria de conjuntos, essas relações podem ser escritas da seguinte maneira:
![]()
Radiciação é a operação que realizamos quando queremos descobrir qual o número que multiplicado por ele mesmo uma determinada quantidades de vezes dá um valor que conhecemos.
Exemplo
Qual é o número que multiplicado por ele mesmo 3 vezes dá como resultado 125?
Por tentativa podemos descobrir que:
5 x 5 x 5 = 125
Logo, o 5 é o número que estamos procurando.
Símbolo da Radiciação
Para indicar a radiciação usamos a seguinte notação:

Sendo,
n o índice do radical. Indica quantas vezes o número que estamos procurando foi multiplicado por ele mesmo.
X o radicando. Indica o resultado da multiplicação do número que estamos procurando por ele mesmo.
Quando não aparecer nenhum valor no índice do radical, o seu valor é igual a 2. Essa raiz é chamada de raiz quadrada.
A raiz de índice igual a 3 também recebe um nome especial e é chamada de raiz cúbica.
Exemplos
3√27 (Lê-se raiz cúbica de 27)
5√32 (Lê-se raiz quinta de 32)
√400 (Lê-se raiz quadrada de 400)
Propriedades da Radiciação
As propriedades da radiciação são muito úteis quando necessitamos simplificar radicais.

Radiciação e Potenciação
A radiciação é a operação matemática inversa da potenciação. Desta forma, podemos encontrar o resultado de uma raiz buscando a potenciação que tem como resultado a raiz proposta.
Exemplos
a) √81= 9, pois sabemos que 92 = 81
b) 4√10 000 = 10, pois sabemos que 104 = 10 000
Saiba mais sobre a potenciação e a radiciação.
Simplificação de Radicais
Muitas vezes não sabemos de forma direta o resultado da radiciação ou o resultado não é um número inteiro. Neste caso, podemos simplificar o radical.
Para fazer a simplificação devemos seguir os seguintes passos:
1º) Fatorar o número em fatores primos.
2º) Escrever o número na forma de potência.
3º) Colocar a potência encontrada no radical e dividir por um mesmo número o índice do radical e o expoente da potência (propriedade da radiciação).
Exemplo
Calcule 5√ 243
Primeiro transformar o número 243 em fatores primos:

243 = 3 x 3 x 3 x 3 x 3 = 35
Depois colocar o resultado na raiz:
5√243 = 5√35
Para simplificar, devemos dividir o índice e o expoente da potenciação por um mesmo número. Quando isso não for possível, significa que o resultado da raiz não é um número inteiro.
5 : 5√35 : 5, note que ao dividir o índice por 5 o resultado é igual a 1, desta forma cancelamos o radical.
Assim,
5√243 = 3
Racionalização de Denominadores
A racionalização de denominadores consiste em transformar uma fração que apresenta um número irracional no denominador, em uma fração equivalente com denominador racional.
Exemplos

Operações com Radicais
Soma e Subtração
Para somar ou subtrair devemos identificar se os radicais são semelhantes, ou seja, se apresentam índice e radicando iguais.
1º caso – Radicais semelhantes
Para somar ou subtrair radicais semelhantes, devemos repetir o radical e somar ou subtrair seus coeficientes.
Exemplos
a) 20 6√ 3 + 103 6√ 3 = 123 6√ 3
b) 5√13 – 43 5√13 = 13 5√13
c) 2 3√5 + 8 3√ 5 – 4 3√5 = 6 3√5
2º caso – Radicais semelhantes após simplificação
Neste caso, devemos inicialmente simplificar os radicais para se tornarem semelhantes. Depois, faremos como no caso anterior.
Exemplos
a) 8 √ 6 + 9 √ 24 = 8 √ 6 + 9 √ (22. 2. 3) = 8 √ 6 + (9.2) √ 6 = 26 √ 6
b) 5 3√ 81 - 4 3√ 3 = 5 3√ (33. 3) - 4 3√ 3 = 5.3 3√ 3 - 4 3√ 3 = 15 3√ 3 – 4 3√ 3 = 11 3√ 3
3º caso – Radicais não são semelhantes
Calculamos os valores dos radicais e depois efetuamos a soma ou a subtração.
Exemplos
a) √81 + √25 = 9 + 5 = 14
b) √5 - √2 = 2,24 - 1,41 = 0,82 (valores aproximados, pois a raiz quadrada de 5 e de 2 são números irracionais)
Multiplicação e Divisão
1º caso - Radicais com mesmo índice
Repete a raiz e multiplica ou divide os radicandos.
Exemplos
a) 3√ 7 . 3√ 4 = 3√(7 .4) = 3√28
b) 5√ 194 : 5√ 97 = 5√ (194 : 97) = 5√2
2º caso - Radicais com índices diferentes
Primeiro, devemos reduzir ao mesmo índice, depois podemos multiplicar ou dividir os radicandos.
Exemplos
a) 3√ 6 . √ 3 = 3x2√ 61x2 . 2x3√ 31x3 = 6√ 36 . 6√ 27 = 6√ 972
b) 3√ 4 : 5√ 8 = 3x5√ 41x5 : 5x3√ 81x3 = 15√ (1024 : 512) = 15√ 2
A equação do 2º grau é caracterizada por um polinômio de grau 2, ou seja, um polinômio do tipo ax2+bx+c, em que a, b e c são números reais. Ao resolvermos uma equação de grau 2, estamos interessados em encontrar valores para a incógnita x que torne o valor da expressão igual a 0, que são chamadas de raízes, isto é, ax2 + bx +c = 0.
A equação de 2º grau pode ser representada por ax²+bx+c=0, em que os coeficientes a, b e c são números reais, com a ≠ 0.
→ Exemplos
a) 2x2 +4x – 6 = 0 → a = 2; b =4 e c = – 6
b) x2 – 5x + 2 = 0 → a =1; b= – 5 e c = 2
c) 0,5x2 + x –1 = 0 → a = 0,5; b = 1 e c = –1
A equação do 2º grau é classificada como completa quando todos os coeficientes são diferentes de 0, ou seja, a ≠ 0, b ≠ 0 e c ≠ 0.
A equação do 2º grau é classificada como incompleta quando o valor dos coeficientes b ou c são iguais a 0, isto é, b = 0 ou c = 0.
→ Exemplos
a) 2x2 – 4 = 0 → a = 2; b = 0 e c= – 4
b) -x2 + 3x = 0 → a = – 1; b = 3 e c = 0
c) x2 = 0 → a = 1; b =0 e c =0
Atenção: o valor do coeficiente a nunca é igual a 0, caso isso ocorra, a equação deixa de ser do 2º grau.
Como resolver equações de 2º grau?
A solução de uma equação do 2º grau ocorre, quando as raízes são encontradas, ou seja, os valores atribuídos a x . Esses valores de x devem tornar a igualdade verdadeira, isto é, ao substituir o valor de x na expressão, o resultado deve ser igual a 0.
→ Exemplo
Considerando a equação x2 – 1 = 0 temos que x’ = 1 e x’’ = – 1 são soluções da equação, pois substituindo esses valores na expressão, temos uma igualdade verdadeira. Veja:
x2 – 1 = 0
(1)2 – 1 = 0 e (–1)2 – 1 = 0
Para encontrar a solução de uma equação, é preciso analisar se a equação é completa e incompleta e selecionar qual método será utilizado.
-
Método de solução para equações do tipo ax²+ c = 0
O método para determinar a solução de equações incompletas que possuem b=0 consiste em isolar a incógnita x, assim:
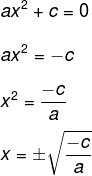
→ Exemplo
Encontre as raízes da equação 3x2 – 27 = 0.
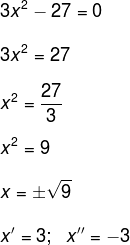
Se quiser saber mais sobre esse método, acesse: equação incompleta do 2º grau com coeficiente b nulo.
-
Método de solução para equações do tipo ax2 + bx = 0
O método para determinar as possíveis soluções de uma equação com c =0, consiste em utilizar a fatoração por evidência. Veja:
ax2 + bx = 0
x·(ax + b) = 0
Ao observar a última igualdade, é notável que há uma multiplicação e que para o resultado ser 0, é necessário que, pelo menos, um dos fatores seja igual a 0.
x·(ax + b) = 0
x = 0 ou ax + b = 0
Assim, a solução da equação é dada por:
![]()
→ Exemplo
Determine a solução da equação 5x2 – 45x = 0
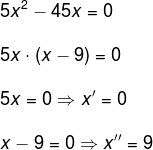
Se quiser saber mais sobre esse método, acesse: equação incompleta do 2º grau com coeficiente c nulo.
-
Método de solução para equações completas
O método conhecido como método de Bhaskara ou fórmula de Bhaskara aponta que as raízes de uma equação do 2º grau do tipo ax2 + bx + c = 0 é dada pela seguinte relação:
![]()
→ Exemplo
Determine a solução da equação x2 – x – 12 = 0.
Note que os coeficientes da equação são: a = 1; b= – 1 e c = – 12. Substituindo esses valores na fórmula de Bhaskara, temos:
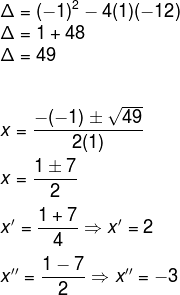
O delta (Δ) recebe o nome de discriminante e note que ele está dentro de uma raiz quadrada e, conforme sabemos, levando em conta os números reais, não é possível extrair raiz quadrada de um número negativo.
Conhecendo o valor do discriminante, podemos realizar algumas afirmações a respeito da solução da equação do 2º grau:
→ discriminante positivo (Δ > 0): duas soluções para a equação;
→ discriminante igual a zero (Δ = 0): as soluções da equação são repetidas;
→ discriminante negativo (Δ < 0): não admite solução real.
Sistemas de equações do segundo grau
Quando consideramos simultaneamente duas ou mais equações, temos um sistema de equações. A solução de um sistema de 2 variáveis é o conjunto de pares ordenados que satisfaz simultaneamente todas as equações envolvidas.
→ Exemplo
Considere o sistema:
![]()
Com os valores: x’ = 2, x’’ = – 2 e y’ = 2, y’’ = – 2 podemos montar pares ordenados que satisfazem as equações do sistema simultaneamente. Veja: (2, 2), (2, – 2), (– 2, 2), (– 2, – 2).
Lembre-se de que um par ordenado é escrito da forma (x, y).
Os métodos para encontrar a solução de um sistema de equações são semelhantes ao de sistemas lineares.
→ Exemplo
Considere o sistema:
![]()
Da equação x – y = 0, vamos isolar a incógnita x, assim:
x – y = 0
x = y
Agora devemos substituir o valor isolado na outra equação, assim:
x2 – x –12 = 0
y2 – y –12 = 0
Utilizando método de Bhaskara, temos que:
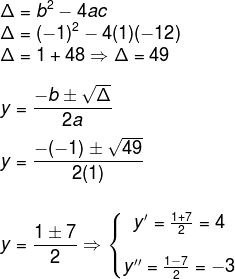
Como x = y, teremos que x’ = y’ e x’’ = y’’. Ou seja:
x’ = 4
x’’ = -3
Assim, os pares ordenados são soluções do sistema (4, 4) e (– 3,– 3).
Leia mais: Sistema de equações do 1º e 2º grau
Exercícios resolvidos
Questão 1 – (ESPM -SP) As soluções da equação abaixo são dois números
![]()
a) primos.
b) positivos.
c) negativos.
d) pares.
e) ímpares.
Solução
Sabemos que os denominadores de uma fração não podem ser iguais a zero, logo x ≠1 e x≠3. E como temos uma igualdade de frações, podemos realizar a multiplicação cruzada, obtendo:
(x+3) · (x+3) = (x – 1) · (3x +1)
x2 + 6x +9 = 3x2 – 2x – 1
x2 – 3x2 + 6x + 2x +9 +1 = 0
(– 1) – 2x2 + 8x +10 = 0 (– 1)
2x2 – 8x – 10 = 0
Dividindo por 2 ambos os lados da equação, temos:
x2 – 4x – 5 = 0
Utilizando a fórmula de Bhaskara segue que:
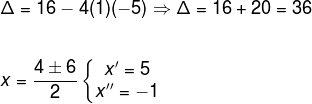
Observe que as raízes da equação são números ímpares.
Alternativa e.
Questão 2 – (UFPI) Um criador de aves verificou que, após colocar (n +2) aves em cada um dos n viveiros disponíveis, sobraria apenas uma ave. O número total de aves, para qualquer valor de n natural, é sempre
a) um número par.
b) um número ímpar.
c) um quadrado perfeito.
d) um número divisível por 3.
e) um número primo.
Solução
A quantidade de aves pode ser encontrada multiplicando o número de viveiros pela quantidade de aves colocada em cada um deles, pelo enunciado do exercício depois de fazer esse processo ainda sobra uma ave, podemos escrever tudo isso da seguinte maneira:
n·(n+2) +1
Realizando a distributividade vamos obter:
n2 + 2n +1
E fatorando esse polinômio segue que:
(n +1)2
Assim, o número toral de aves é sempre um quadrado perfeito para qualquer número natural n.
Alternativa C
O triângulo retângulo possui algumas particularidades relacionadas aos seus lados e ângulos. Considere o triângulo retângulo ABC, veja que AB é a hipotenusa (lado oposto ao ângulo reto e sempre o maior lado do triângulo) e BC e AC são os catetos (lados que formam o ângulo reto).

O teorema de Pitágoras expressa uma das relações de medida desse triângulo:
Em um triângulo retângulo qualquer, a soma dos quadrados das medidas dos catetos é igual ao quadrado da medida da hipotenusa.
a² = b² + c²
Exemplo: Determine a medida de a no triângulo retângulo a seguir:

Utilizando o teorema de Pitágoras, temos:
a² = b² + c²
a² = 5² + 12²
a² = 25 + 144
a² = 169
√a² = √169
a= 13
Existem outras relações métricas no triângulo retângulo que podem ser expressas através da semelhança entre triângulos, veja:
Em um triângulo retângulo qualquer, o quadrado da medida da altura relativa à hipotenusa é igual ao produto das medidas das projeções ortogonais dos catetos sobre a hipotenusa.

∆ HBA ≈ ∆ HAC
HB = HA
HA HC
m = h → h² = m. n
h n
Por Camila Garcia
Graduada em Matemática

